System.Numerics.Vector is a library provided by .Net (as a nuget package), which tries to leverage SIMD instruction on target hardware. It exposes a few value types, such as Vector<T>, which are recognized by RyuJIT as intrinsics. Hybridizer however delivers full SIMD instructions potential without the burden of writing vector code.
Month: June 2017
From C# to SIMD : Numerics.Vector and Hybridizer
System.Numerics.Vector is a library provided by .Net (as a nuget package), which tries to leverage SIMD instruction on target hardware. It exposes a few value types, such as Vector<T>, which are recognized by RyuJIT as intrinsics.
Supported intrinsics are listed in the core-clr github repository.
This allows C# SIMD acceleration, as long as code is modified to use these intrinsic types, instead of scalar floating point elements.
On the other hand, Hybridizer aims to provide those benefits without being intrusive in the code (only metadata is required).
We naturally wanted to test if System.Numerics.Vector delivers good performance, compared to Hybridizer.
We measured that Numerics.Vector provides good speed-up over C# code as long as no transcendental function is involved (such as Math.Exp), but still lags behind Hybridizer. Because of the lack of some operators and mathematical functions, Numerics can also generate really slow code (when AVX pipeline is broken). In addition, code modification is a heavy process, and can’t easily be rolled back.
We wrote and ran two benchmarks, and for each of them we have four versions:
- Simple C# scalar code
- Numerics.Vector
- Simple C# scalar code, hybridized
- Numerics.Vector, hybridized
Processor is a core i7-4770S @ 3.1GHz (max measured turbo in AVX mode being 3.5GHz). Peak flops is 224 GFlop/s, or 112 GCFlop/s, if we count FMA as one (since our processor supports it).
Compute bound benchmark
This is a compute-intensive benchmark. For each element of a large double precision array (8 millions elements: 67MBytes), we iterate twelve times the computation of an exponential’s Taylor expansion (expm1). This is largely enough to enter the compute-bound world, by hiding memory operations latency behind a full bunch of floatin point operations.
Scalar code is simply:
[MethodImpl(MethodImplOptions.AggressiveInlining)]
public static double expm1(double x)
{
return ((((((((((((((15.0 + x)
* x + 210.0)
* x + 2730.0)
* x + 32760.0)
* x + 360360.0)
* x + 3603600.0)
* x + 32432400.0)
* x + 259459200.0)
* x + 1816214400.0)
* x + 10897286400.0)
* x + 54486432000.0)
* x + 217945728000.0)
* x + 653837184000.0)
* x + 1307674368000.0)
* x * 7.6471637318198164759011319857881e-13;
}
[MethodImpl(MethodImplOptions.AggressiveInlining)]
public static double twelve(double x)
{
return expm1(expm1(expm1(expm1(expm1(expm1(expm1(expm1(expm1(expm1(expm1(x)))))))))));
}
on which we added the AggressiveInlining attribute to help RyuJit to merge operations at JIT time.
The Numerics.Vector version of the code is quite the same:
[MethodImpl(MethodImplOptions.AggressiveInlining)]
public static Vector<double> expm1(Vector<double> x)
{
return ((((((((((((((new Vector<double>(15.0) + x)
* x + new Vector<double>(210.0))
* x + new Vector<double>(2730.0))
* x + new Vector<double>(32760.0))
* x + new Vector<double>(360360.0))
* x + new Vector<double>(3603600.0))
* x + new Vector<double>(32432400.0))
* x + new Vector<double>(259459200.0))
* x + new Vector<double>(1816214400.0))
* x + new Vector<double>(10897286400.0))
* x + new Vector<double>(54486432000.0))
* x + new Vector<double>(217945728000.0))
* x + new Vector<double>(653837184000.0))
* x + new Vector<double>(1307674368000.0))
* x * new Vector<double>(7.6471637318198164759011319857881e-13);
}
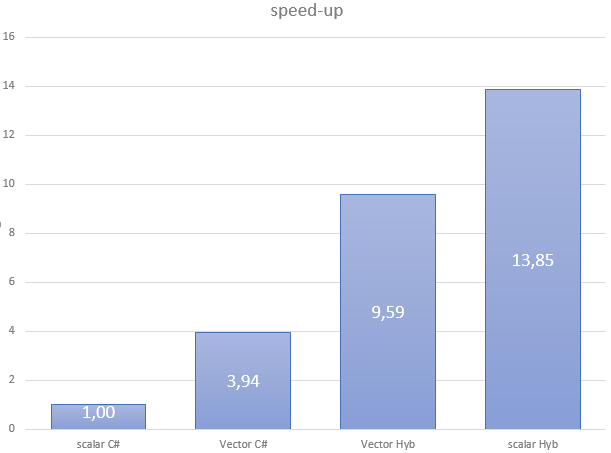
The four versions of this code give the following performance results:
| Flavor | Scalar C# | Vector C# | Vector Hyb | Scalar Hyb |
| GCFlop/s | 4.31 | 19.95 | 41.29 | 59.65 |
As stated, Numerics.Vector delivers a close to 4x speedup from scalar. However, performance is far from what we reach with the Hybridizer. If we look at generated assembly, it’s quite clear why:
vbroadcastsd ymm0,mmword ptr [7FF7C2255B48h] vbroadcastsd ymm1,mmword ptr [7FF7C2255B50h] vbroadcastsd ymm2,mmword ptr [7FF7C2255B58h] vbroadcastsd ymm3,mmword ptr [7FF7C2255B60h] vbroadcastsd ymm4,mmword ptr [7FF7C2255B68h] vbroadcastsd ymm5,mmword ptr [7FF7C2255B70h] vbroadcastsd ymm7,mmword ptr [7FF7C2255B78h] vbroadcastsd ymm8,mmword ptr [7FF7C2255B80h] vaddpd ymm0,ymm0,ymm6 vmulpd ymm0,ymm0,ymm6 vaddpd ymm0,ymm0,ymm1 vmulpd ymm0,ymm0,ymm6 vaddpd ymm0,ymm0,ymm2 vmulpd ymm0,ymm0,ymm6 vaddpd ymm0,ymm0,ymm3 vmulpd ymm0,ymm0,ymm6 vaddpd ymm0,ymm0,ymm4 vmulpd ymm0,ymm0,ymm6 vaddpd ymm0,ymm0,ymm5 vmulpd ymm0,ymm0,ymm6 vaddpd ymm0,ymm0,ymm7 vmulpd ymm0,ymm0,ymm6 vaddpd ymm0,ymm0,ymm8 vmulpd ymm0,ymm0,ymm6 ; repeated
Fused multiply add are not reconstructed, and constant operands are reloaded from constant pool at each expm1 invokation. This leads to high registry pressure (for constants), where memory operands could save some.
Here is what the Hybridizer generates from scalar code:
vaddpd ymm1,ymm0,ymmword ptr [] vfmadd213pd ymm1,ymm0,ymmword ptr [] vfmadd213pd ymm1,ymm0,ymmword ptr [] vfmadd213pd ymm1,ymm0,ymmword ptr [] vfmadd213pd ymm1,ymm0,ymmword ptr [] vfmadd213pd ymm1,ymm0,ymmword ptr [] vfmadd213pd ymm1,ymm0,ymmword ptr [] vfmadd213pd ymm1,ymm0,ymmword ptr [] vfmadd213pd ymm1,ymm0,ymmword ptr [] vfmadd213pd ymm1,ymm0,ymmword ptr [] vfmadd213pd ymm1,ymm0,ymmword ptr [] vfmadd213pd ymm1,ymm0,ymmword ptr [] vfmadd213pd ymm1,ymm0,ymmword ptr [] vfmadd213pd ymm1,ymm0,ymmword ptr [] vmulpd ymm0,ymm0,ymm1<br /> vmulpd ymm0,ymm0,ymmword ptr [] vmovapd ymmword ptr [rsp+0A20h],ymm0 ; repeated
This reconstructs fused multiply-add, and leverages memory operands to save registers.
Why are we not to peak performance (112GCFlops)? That is because Haswell has two pipelines for FMA, and a latency of 5 (see intel intrinsic guide. To reach peak performance, we would need to interleave 2 independant FMA instruction at each cycle. This could be done by reordering instructions, since reorder buffer is not long enough to execute instructions too far in the pipeline. LLVM, our backend compiler, is not capable of such reordering. To get better performance, we unfortunately have to write assembly by hand (which is not exactly what a C# programmer expects to do in the morning).
Invoke transcendentals
In this second benchmark, we need to compute the exponential of all the components of a vector. To do that, we invoke Math.Exp.
Scalar code is:
[EntryPoint]
public static void Apply_scal(double[] d, double[] a, double[] b, double[] c, int start, int stop)
{
int sstart = start + threadIdx.x + blockDim.x * blockIdx.x;
int step = blockDim.x * gridDim.x;
for (int i = sstart; i < stop; i += step)
{
d[i] = a[i] * Math.Exp(b[i]) * Math.Exp(c[i]);
}
}
This function is later called in a
Parallel.For construct.
However, Numerics.Vector does not provide a vectorized exponential function. Therefore, we have to write our own:
[IntrinsicFunction("hybridizer::exp")]
[MethodImpl(MethodImplOptions.AggressiveInlining)]
public static Vector<double> Exp(Vector<double> x)
{
double[] tmp = new double[Vector<double>.Count];
for(int k = 0; k < Vector<double>.Count; ++k)
{
tmp[k] = Math.Exp(x[k]);
}
return new Vector<double>(tmp);
}
As a glance, we can see the problems: each exponential will first break the AVX context (which cost tens of cycles), and trigger 4 function calls instead of one.
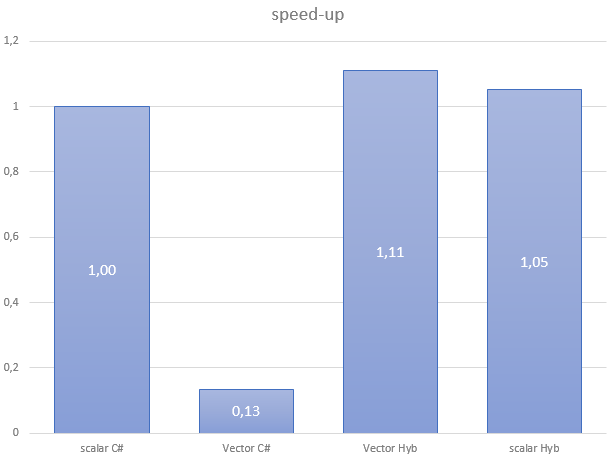
With no surprise, this code performs really badly:
| Flavor | Scalar C# | Vector C# | Vector Hyb | Scalar Hyb |
| GB/s | 13.42 | 1.80 | 14.91 | 14.13 |
If we look at the generated assembly, it confirms what we suspected (context switched, and ymm register splitting):
vextractf128 xmm9,ymm6,1 vextractf128 xmm10,ymm7,1 vextractf128 xmm11,ymm8,1 call 00007FF8127C6B80 // exp vinsertf128 ymm8,ymm8,xmm11,1 vinsertf128 ymm7,ymm7,xmm10,1 vinsertf128 ymm6,ymm6,xmm9,1
Branching
Branch are expressed using if or ternary operators in scalar code. However, those are not available in Numerics.Vector, since the code is manually vectorized.
Branches must be expressed using ConditionalSelect, which leads to code:
public static Vector<double> func(Vector<double> x)
{
Vector<long> mask = Vector.GreaterThan(x, one);
Vector<double> result = Vector.ConditionalSelect(mask, x, one);
return result;
}
As we can see, expressing conditions with Numerics.Vector is not intuitive, intrusive, and bug prone. It’s actually the same as writing AVX compiler intrinsics in C++. On the other hand, Hybridizer supports conditions, which allow you to write the above code this way:
[Kernel]
public static double func(double x)
{
if (x > 1.0)
return x;
return 1.0;
}
Conclusion
Numerics.Vector gives easily reasonable performances on simple code (no branches, no function calls). Speed-up is what we expect (vector unit width) on simple code. However, it’s time-consuming and error-prone to express conditions, and performance is completely broken as soon as some Jitter Intrinsic is missing (such as exponential).
Image processing on a GPU with AForge
AForge is a popular .Net library for image processing and computer vision. It features a lot of image filters, noise generators, or other image-related algorithms.
Since it’s written in C#, and given the very parallel nature of most of image processing algorithms, we tried to hybridize some of them.
AForge code make heavy use of dot net unsafe, which is supported by the Hybridizer.
We chose two examples to illustrate hybridizer’s capabilities. First is Perlin noise, a highly compute intensive noise generator, and second is AdaptiveSmoothing, a latency bound image filter.
Perlin noise
Perlin noise is written for double precison in AForge, and we test on a GTX 1080 Ti, which has almost no double precision arithmetic units. We therefore first cloned the Perlin noise algorithm and made a PerlinNoiseFloat class, in which we just replaced “double” by “float”, without changing a single bit of the code structure or algorithm implementation.
However, Perlin noise makes use of Cosine function, which is only available for double in C#. We replaced Math.Cos by an Intrinsic function, mapped to cosf from C99 standard:
[IntrinsicFunction("cosf")]
public static float cosf(float x)
{
return (float)Math.Cos(x);
}
The main function is a simple cuda-like loop, other mathematical functions being mapped to their C99 counterparts with the default builtin file:
[EntryPoint]
public static void ComputePerlin(PerlinNoiseFloat noise, float[] image, int width, int height)
{
for (int y = threadIdx.y + blockDim.y * blockIdx.y; y < height; y += blockDim.y * gridDim.y)
{
for (int x = threadIdx.x + blockDim.x * blockIdx.x; x < width; x += blockDim.x * gridDim.x)
{
image[y*width + x] = Math.Max(0.0f, Math.Min(1.0f, noise.Function2D(x, y) * 0.5f + 0.5f));
}
}
}
PerlinNoiseFloat is defined in a separate assembly (AForge.Imaging) in which we didn’t put any custom attributes. Given noise.Function2D is invoked by an EntryPoint, hybridizer infers that it must be a __device__ function, and that code should be generated (call graph is walked by the Hybridizer).
We then invoke this function by wrapping the parent type using HybRunner:
PerlinNoiseFloat noise = new PerlinNoiseFloat();
noise.Octaves = 16;
const int height = 2048;
const int width = 2048;
// generate clouds effect
float[] texture = new float[height*width];
HybRunner runner = HybRunner.Cuda("TestRun_CUDA.dll").SetDistrib(32, 32, 16, 16, 1, 0);
dynamic wrapped = runner.Wrap(new Program());
wrapped.ComputePerlin(noise, texture, width, height);
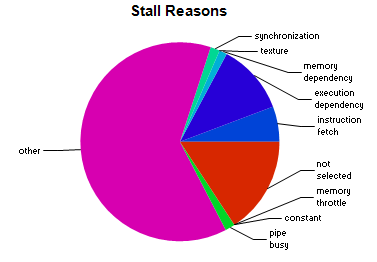
This saturates the compute units of the 1080 Ti, as we can see in this nvvp report:
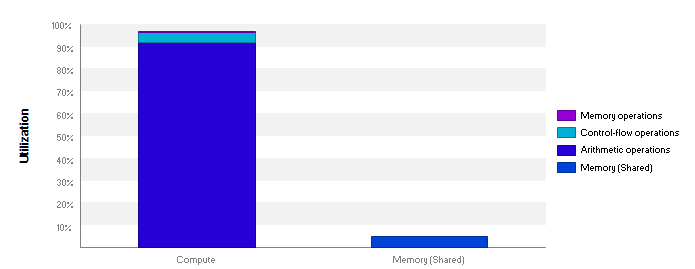
Stall reasons being mostly Other and Not Selected, for which we hqve no documentation to address:
Adaptive Smoothing
Adaptive smoothing is a noise removal filter which preserves edges. The kernel operates on 9 pixels (the 8 around, and the current one) and is described here.
To run this filter on the GPU, we had to slightly modify AForge code, since it was really designed and optimized for single-thread CPU. For example, the main loop was written this way:
for ( int y = startYP2; y < stopYM2; y++ )
{
src += pixelSize2;
dst += pixelSize2;
for(int x = startXP2; x < stopXM2; x++)
{
for(int i = 0; i < pixelSize; i++, src++, dst++)
// operations
in which pointers src and dst are incremented. This can’t be multithreaded, or hybridized, since each thread can’t rely on each other to know where to work.
We changed that loop by a CUDA-like loop, with in place addresses calculation:
int ystart = threadIdx.y + blockIdx.y * blockDim.y;
int yinc = blockDim.y * gridDim.y;
int xstart = threadIdx.x + blockIdx.x * blockDim.x;
int xinc = blockDim.x * gridDim.x;
for (int y = startYP2 + ystart; y < stopYM2; y += yinc)
{
for (int x = startXP2 + xstart; x < stopXM2; x += xinc)
{
byte* vsrc = src + srcInitOffset + ...
byte* vdst = dst + dstInitOffset + ...
for(int i = 0; i < pixelSize; ++i)
// operations
We also had to expose single precision exponential function through intrinsic function, mapped to expf from C99 standard:
[IntrinsicFunction("expf")]
public static float expf(float x)
{
return (float)Math.Exp(x);
}
and do some manual memory management (cudaMalloc/cudaFree/cudaMemcpy). Indeed, unlike arrays, pointers cannot be automatically marshalled (memory size is unknown).
The main loop (ready for hybridization) looks this way:
[EntryPoint]
public static unsafe void Apply(int srcStride, int dstStride, int pixelSize, int srcOffset, int dstOffset, int startX, int startY, int stopX, int stopY, float invf, byte* src, byte* dst)
{
int startXP2 = startX + 2;
int startYP2 = startY + 2;
int stopXM2 = stopX - 2;
int stopYM2 = stopY - 2;
int pixelSize2 = 2 * pixelSize;
int srcInitOffset = srcStride * 2 + (startY * srcStride + startX * pixelSize) + pixelSize2;
int dstInitOffset = dstStride * 2 + (startY * dstStride + startX * pixelSize) + pixelSize2;
int incx = pixelSize;
int incsrcy = srcOffset + 2 * pixelSize2;
int incdsty = dstOffset + 2 * pixelSize2;
<pre><code>for (int y = startYP2 + threadIdx.y + blockIdx.y * blockDim.y; y < stopYM2; y += blockDim.y * gridDim.y)
{
for (int x = startXP2 + threadIdx.x + blockDim.x * blockIdx.x; x < stopXM2; x += blockDim.x * gridDim.x)
{
byte* vsrc = src + srcInitOffset
+ (y - startYP2) * incsrcy + (y - startYP2) * (stopXM2 - startXP2) * incx
+ (x - startXP2) * incx;
byte* vdst = dst + dstInitOffset
+ (y - startYP2) * incdsty + (y - startYP2) * (stopXM2 - startXP2) * incx
+ (x - startXP2) * incx;
for (int i = 0; i < pixelSize; i++, vsrc++, vdst++)
{
// gradient and weights
float gx, gy, weight, weightTotal, total;
weightTotal = 0;
total = 0;
// original formulas for weight calculation:
// w(x, y) = exp( -1 * (Gx^2 + Gy^2) / (2 * factor^2) )
// Gx(x, y) = (I(x + 1, y) - I(x - 1, y)) / 2
// Gy(x, y) = (I(x, y + 1) - I(x, y - 1)) / 2
//
// here is a little bit optimized version
// x - 1, y - 1
gx = vsrc[-srcStride] - vsrc[-pixelSize2 - srcStride];
gy = vsrc[-pixelSize] - vsrc[-pixelSize - 2 * srcStride];
weight = expf((gx * gx + gy * gy) * invf);
total += weight * vsrc[-pixelSize - srcStride];
weightTotal += weight;
// x, y - 1
gx = vsrc[pixelSize - srcStride] - vsrc[-pixelSize - srcStride];
gy = vsrc[0] - vsrc[-2 * srcStride];
weight = expf((gx * gx + gy * gy) * invf);
total += weight * vsrc[-srcStride];
weightTotal += weight;
// x + 1, y - 1
gx = vsrc[pixelSize2 - srcStride] - vsrc[-srcStride];
gy = vsrc[pixelSize] - vsrc[pixelSize - 2 * srcStride];
weight = expf((gx * gx + gy * gy) * invf);
total += weight * vsrc[pixelSize - srcStride];
weightTotal += weight;
// x - 1, y
gx = vsrc[0] - vsrc[-pixelSize2];
gy = vsrc[-pixelSize + srcStride] - vsrc[-pixelSize - srcStride];
weight = expf((gx * gx + gy * gy) * invf);
total += weight * vsrc[-pixelSize];
weightTotal += weight;
// x, y
gx = vsrc[pixelSize] - vsrc[-pixelSize];
gy = vsrc[srcStride] - vsrc[-srcStride];
weight = expf((gx * gx + gy * gy) * invf);
total += weight * (vsrc[0]);
weightTotal += weight;
// x + 1, y
gx = vsrc[pixelSize2] - vsrc[0];
gy = vsrc[pixelSize + srcStride] - vsrc[pixelSize - srcStride];
weight = expf((gx * gx + gy * gy) * invf);
total += weight * vsrc[pixelSize];
weightTotal += weight;
// x - 1, y + 1
gx = vsrc[srcStride] - vsrc[-pixelSize2 + srcStride];
gy = vsrc[-pixelSize + 2 * srcStride] - vsrc[-pixelSize];
weight = expf((gx * gx + gy * gy) * invf);
total += weight * vsrc[-pixelSize + srcStride];
weightTotal += weight;
// x, y + 1
gx = vsrc[pixelSize + srcStride] - vsrc[-pixelSize + srcStride];
gy = vsrc[2 * srcStride] - vsrc[0];
weight = expf((gx * gx + gy * gy) * invf);
total += weight * vsrc[srcStride];
weightTotal += weight;
// x + 1, y + 1
gx = vsrc[pixelSize2 + srcStride] - vsrc[srcStride];
gy = vsrc[pixelSize + 2 * srcStride] - vsrc[pixelSize];
weight = expf((gx * gx + gy * gy) * invf);
total += weight * vsrc[pixelSize + srcStride];
weightTotal += weight;
// save destination value
*vdst = (weightTotal == 0.0F) ? vsrc[0] : (byte)min(total / weightTotal, 255.0F);
}
}
}
</code></pre>
}
We run this filter on a fullHD image (1080p):

and we get the following level of performance:
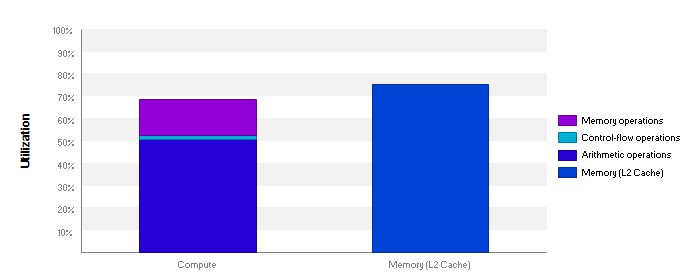
with 98.2% of warp execution efficiency.
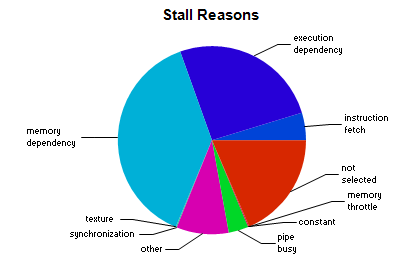
Stall reasons are:
mostly memory dependency and execution dependency.
Occupancy limiter is registers with 40 registers per thread.
Given both compute and memory are highly used, the kernel is memory-latency bound, which is difficult to optimize further without being really intrusive in the code. We could get some improvement by processing a group of pixels simultaneously, or make use of Surfaces to benefit from 128 bits loads and stores in GPU memory.
Conclusion
In this post we demonstrated how we can take production-level C# code (with advanced features such as unsafe code) and run it on a GPU with the Hybridizer. In the case of Perlin, we don’t even have to modify the third-part library, since writing a kernel in our application will make Hybridizer automatically walk through dependencies and generate the appropriate code.
This code is completely compute bound on a GPU, and that is what we observe. In the other case (Adaptive smoothing), we solely had to modify the pointer indexing calculation scheme which is anyway necessary to make loop iterations independent. This change would be required to benefit from any modern hardware.
Hybridize A Large Image Processing Library
AForge is a great Image Processing and Vision .Net library.
We developed a few example applications making use of AForge and Hybridizer. Those two examples are:
- A kernel function in application code which triggers the hybridization of AForge itself. This shows that dependencies are pulled by the Hybridizer with no user intervention. On Perlin noise code, we reach peak compute performance on a 1080 Ti.
- Adaptive smoothing. We had to change AForge code to enable parallel processing (addresses computation). We then call it from a plain C# application code. We have therefore an hybridized library used transparently from the application code. Kernel appears to be memory-latency bound on a 1080 Ti.