Hybridizer supports C# generics (for a long time). However, managed generics are resolved at runtime, introducing a significant performance penalty.
Hybridizer map them to C++ templates (which are resolved at compile time), therefore dramatically improving performance.
This blog post gives an example of generic code on a quite fun mathematical example.
Month: July 2017
Generics and virtual functions
Hybridizer supports generics and virtual functions. These concepts allow writing flexible code with type parameters, defering actual behavior resolution to type instanciation by client code. These are fondamental features of modern languages, easing encapsulation, code factorization and concepts expression.
However in C#, type parameters are resolved at runtime, which comes with a significant performance penalty. Hybridizer maps them to C++ templates, which are resolved at compile time. As such, templates allow inlining and interprocedural optimization as in plain C code. Performance penalty is therefore inexisting.
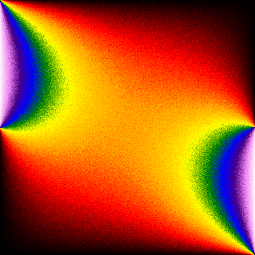
As an example, we will demonstrate usage of generics on a fun mathematical example : the resolution of heat equation with random walks.
Mathematic background
Given a connected bounded 2D domain \(\Omega\) in \(\mathbb{R}^2\), its border \(\partial \Omega\) and a function \(f\in: \textrm{L}^2(\partial\Omega)\), we search \(u\) such as:
\(
\begin{array}{lcl}
\Delta u = 0 & \textrm{on} & \Omega\\
u = f & \textrm{on} & \partial\Omega
\end{array}
\)
Classic ways to numerically solve this problem involve finite elements or similar discretization methods which come with different regularity constraits on \(\partial\Omega\).
It happens we can solve it using montecarlo methods by launching brownian motions. For each point \((x, y)\) in \(\Omega\) we launch \(N\) random walks. For each random walk, we wait until it reaches \(\partial\Omega\) and sample the temperature at exit point. We then sum all those exit temperatures and divide by \(N\) to get the numerical solution :
This method is quite slow (compared to finite elements or similar). But it has some advantages:
- It can easily be distributed among many threads (all points are independants)
- It’s possible to compute the solution at a specific location
- \(\Omega\) has almost no regularity constraint (external cone)
- Absolutely no memory footprint (except for the solution)
- It works similarly in higher dimensions
Full explanations can be found on this old research report (in french).
Code
We structured our code as would be a generic mathematical solver. The main class is MonteCarloHeatSolver, which takes a I2DProblem to solve it.
This code is generic and solves a problem described by an interface:
public class MonteCarloHeatSolver
{
I2DProblem _problem;
public MonteCarloHeatSolver(I2DProblem problem)
{
_problem = problem;
}
[EntryPoint]
public void Solve()
{
int stopX = _problem.MaxX();
int stopY = _problem.MaxY();
for (int j = 1 + threadIdx.y + blockIdx.y * blockDim.y; j < stopY; j += blockDim.y * gridDim.y) {
for (int i = 1 + threadIdx.x + blockIdx.x * blockDim.x; i < stopX; i += blockDim.x * gridDim.x) {
float2 position;
position.x = i;
position.y = j;
_problem.Solve(position);
}
}
}
}
where actual resolution (geometry related) is deferred to a
I2DProblem. The call to Solve (virtual) won’t be matched to templates. But the Hybridizer will handle this and dispatch this call correctly at runtime. This will cost a vtable lookup, but only once per thread. Performance critical code is in the random walk and the boundary conditions, which are generic parameters of the 2D problem.
An example of C# code instanciation can be:
var problem = new SquareProblem<SimpleWalker, SimpleBoundaryCondition>(N, iterCount); var solver = new MonteCarloHeatSolver(problem); solver.Solve();
We then have two interfaces describing random walks and boundary conditions :
[HybridTemplateConcept]
public interface IRandomWalker
{
[Kernel]
void Init();
[Kernel]
void Walk(float2 f, out float2 t);
}
[HybridTemplateConcept]
public interface IBoundaryCondition
{
[Kernel]
float Temperature(float x, float y);
}
These interfaces are decorated with
[HybridTemplateConcept] which tells the Hybridizer that these types will be used as type parameters. They can be extended by actual classes such as:
public struct SimpleBoundaryCondition : IBoundaryCondition
{
[Kernel]
public float Temperature(float x, float y)
{
if ((x >= 1.0F && y >= 0.5F) || (x <= 0.0F && y <= 0.5F))
return 1.0F;
return 0.0F;
}
}
Generic types using these interfaces have to tell the hybridizer how they want it to generate template code from generics. This is again done by using attributes:
For example:
[HybridRegisterTemplate(Specialize = typeof(SquareProblem<SimpleWalker, SimpleBoundaryCondition>))]
public class SquareProblem<TRandomWalker, TBoundaryCondition>: I2DProblem
where TRandomWalker : struct, IRandomWalker
where TBoundaryCondition: struct, IBoundaryCondition
{
// other interface methods implementations
// ...
[Kernel]
public void Solve(float2 position)
{
TRandomWalker walker = default(TRandomWalker);
TBoundaryCondition boundaryCondition = default(TBoundaryCondition);
walker.Init(); // generic parameter method call -- will be inlined
float temperature = 0.0F;
float size = (float)_N;
for (int iter = 0; iter < _iter; ++iter)
{
float2 f = position;
while (true)
{
float2 t;
walker.Walk(f, out t); // generic parameter method call -- will be inlined
// when on border, break
if(t.x <= 0.0F || t.y >= size || t.x >= size || t.y <= 0.0F)
{
// generic parameter method call -- will be inlined
temperature += boundaryCondition.Temperature((float)t.x * _h, (float)t.y * _h);
break;
}
// otherwise continue walk
f = t;
}
}
_inner[((int)(position.y - 1)) * (_N - 1) + (int)(position.x - 1)] = temperature * _invIter;
}
}
[HybridRegisterTemplate(Specialize = typeof(TetrisProblem<SimpleWalker, TetrisBoundaryCondition>))]
public class TetrisProblem<TRandomWalker, TBoundaryCondition> : I2DProblem
where TRandomWalker : struct, IRandomWalker
where TBoundaryCondition : struct, IBoundaryCondition
{
// actual interface implementation
}
Results
Dispatchant calls
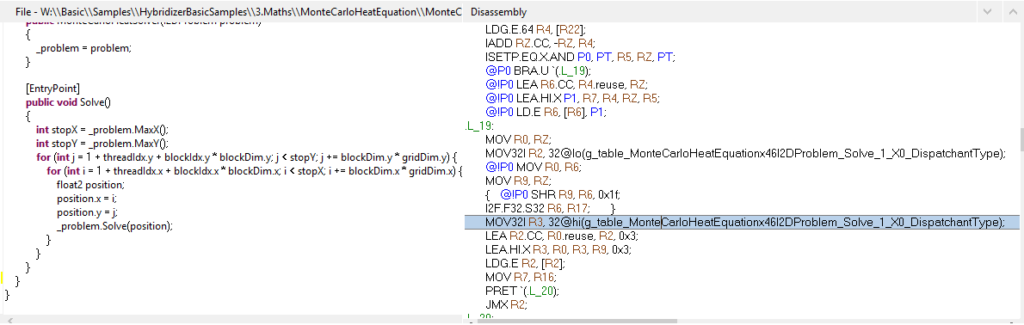
Virtual functions trigger a callvirt in the MSIL.
IL_005e: callvirt instance void MonteCarloHeatEquation.I2DProblem::Solve
Profiling the generated code with nvvp shows us that a vtable is generated by the Hybridizer (ensuring the right method is called):
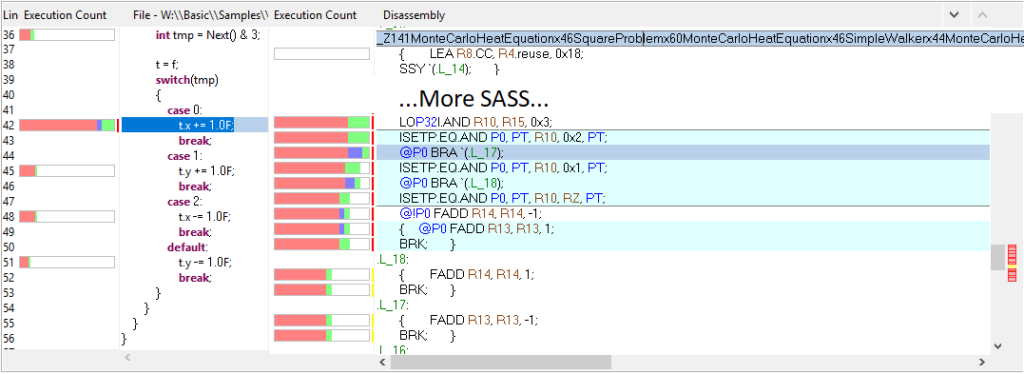
Generics and templates
On the other hand, IRandomWalker and IBoundaryCondition type parameters are mapped to templates. Their methods are therefore inlined, as shown in this nvvp profiling:
By the way: the images above show that your C# code is linked to the sass in the profiler. See our post about debugging and profiling
Conclusion
With few restrictions, you can safely use generics type parameters and dispatchant calls in your C# code. Hybridizer will map that to the correct concept (vtable or template) as your required for.
Dispatchant calls give you full flexibility of an inheritance hierarchy, but come at a performance cost. On the other hand, generics deliver full performance (inlined calls), as long as the right metadata has been provided.
Expm1 Benchmark
This benchmark aims at measuring the floating point performance of the architecture. We use a Taylor expansion of the Expm1 function (exponential of x minus one), at some degree (13 in our case), without any branching. The number of floating point operations, whether it be addition, multiply or fused multiply and add (counted as a single flop in our case) is known ab initio.
We compute the evaluation of that function twelve times to avoid any compute/memory bound unknown hence being sure the calculations are compute bound.
double expm1(double x)
{
return ((((((((((((((15.0 + x)
* x + 210.0)
* x + 2730.0)
* x + 32760.0)
* x + 360360.0)
* x + 3603600.0)
* x + 32432400.0)
* x + 259459200.0)
* x + 1816214400.0)
* x + 10897286400.0)
* x + 54486432000.0)
* x + 217945728000.0)
* x + 653837184000.0)
* x + 1307674368000.0)
* x * 7.6471637318198164759011319857881e-13;
}
We evaluate the function twelve times on a large array of values to exploit parallelism. Depending on the architecture and the flavor of the transformation, vectorization may occur.
We wrote the code in C# and generate target code using Hybridizer. On the other hand, we try to write the best native code for the target architecture. For Intel and IBM targets, code is written in C++ using intrinsics and not raw assembly. For CUDA targets, code is written in plain CUDA. We measure performance of both versions, and see how Hybridizer performs relatively to handwritten code.
| Architecture | Generated | Handwritten | Ratio |
|---|---|---|---|
| NVIDIA- P100 | 1954.7 | 2360.6 | 82.8% |
| NVIDIA – K20C | 505 | 551.1 | 91.6% |
| INTEL – XEON PHI – 7210 | 912.5 | 1003.3 | 90.9% |
| INTEL – Xeon E5 1620 v3 – 3.5 GHz | 60.8 | 84.9 | 71.6% |
| INTEL – Core i7 6700 – 3.4 GHz | 88.1 | 104.5 | 84.3% |
| IBM – POWER8 (2S) | 188.2 | 220.1 | 85.5% |
It can be noticed that on Broadwell (Xeon E5 1620), reached performance is quite far from peak. This is due to the fused-multiply-add instruction latency, which is 5 for a 0.5 throughput. That means we need to enqueue 10 independent instructions to saturate the pipeline. None of the back-end compilers we tried was capable of correctly interleave enough instructions. To reach peak on those architectures, it seems mandatory to write raw assembly. This will be further detailed in a dedicated blog post.