Hybridizer supports C# generics (for a long time). However, managed generics are resolved at runtime, introducing a significant performance penalty.
Hybridizer map them to C++ templates (which are resolved at compile time), therefore dramatically improving performance.
This blog post gives an example of generic code on a quite fun mathematical example.
Author: regis portalez
Generics and virtual functions
Hybridizer supports generics and virtual functions. These concepts allow writing flexible code with type parameters, defering actual behavior resolution to type instanciation by client code. These are fondamental features of modern languages, easing encapsulation, code factorization and concepts expression.
However in C#, type parameters are resolved at runtime, which comes with a significant performance penalty. Hybridizer maps them to C++ templates, which are resolved at compile time. As such, templates allow inlining and interprocedural optimization as in plain C code. Performance penalty is therefore inexisting.
As an example, we will demonstrate usage of generics on a fun mathematical example : the resolution of heat equation with random walks.
Mathematic background
Given a connected bounded 2D domain \(\Omega\) in \(\mathbb{R}^2\), its border \(\partial \Omega\) and a function \(f\in: \textrm{L}^2(\partial\Omega)\), we search \(u\) such as:
\(
\begin{array}{lcl}
\Delta u = 0 & \textrm{on} & \Omega\\
u = f & \textrm{on} & \partial\Omega
\end{array}
\)
Classic ways to numerically solve this problem involve finite elements or similar discretization methods which come with different regularity constraits on \(\partial\Omega\).
It happens we can solve it using montecarlo methods by launching brownian motions. For each point \((x, y)\) in \(\Omega\) we launch \(N\) random walks. For each random walk, we wait until it reaches \(\partial\Omega\) and sample the temperature at exit point. We then sum all those exit temperatures and divide by \(N\) to get the numerical solution :
This method is quite slow (compared to finite elements or similar). But it has some advantages:
- It can easily be distributed among many threads (all points are independants)
- It’s possible to compute the solution at a specific location
- \(\Omega\) has almost no regularity constraint (external cone)
- Absolutely no memory footprint (except for the solution)
- It works similarly in higher dimensions
Full explanations can be found on this old research report (in french).
Code
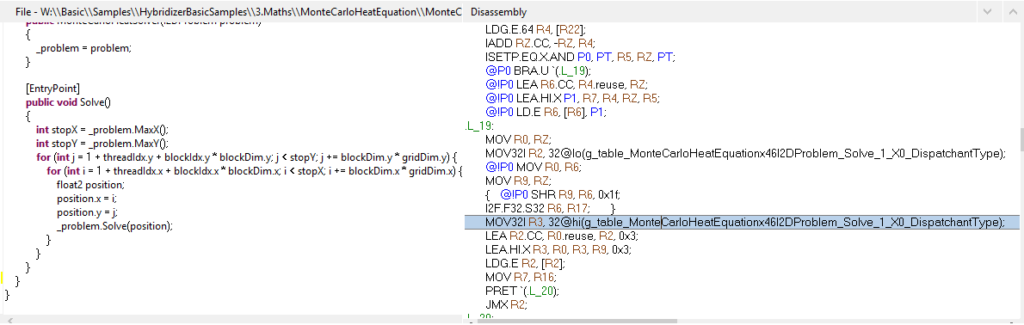
We structured our code as would be a generic mathematical solver. The main class is MonteCarloHeatSolver, which takes a I2DProblem to solve it.
This code is generic and solves a problem described by an interface:
public class MonteCarloHeatSolver
{
I2DProblem _problem;
public MonteCarloHeatSolver(I2DProblem problem)
{
_problem = problem;
}
[EntryPoint]
public void Solve()
{
int stopX = _problem.MaxX();
int stopY = _problem.MaxY();
for (int j = 1 + threadIdx.y + blockIdx.y * blockDim.y; j < stopY; j += blockDim.y * gridDim.y) {
for (int i = 1 + threadIdx.x + blockIdx.x * blockDim.x; i < stopX; i += blockDim.x * gridDim.x) {
float2 position;
position.x = i;
position.y = j;
_problem.Solve(position);
}
}
}
}
where actual resolution (geometry related) is deferred to a
I2DProblem. The call to Solve (virtual) won’t be matched to templates. But the Hybridizer will handle this and dispatch this call correctly at runtime. This will cost a vtable lookup, but only once per thread. Performance critical code is in the random walk and the boundary conditions, which are generic parameters of the 2D problem.
An example of C# code instanciation can be:
var problem = new SquareProblem<SimpleWalker, SimpleBoundaryCondition>(N, iterCount); var solver = new MonteCarloHeatSolver(problem); solver.Solve();
We then have two interfaces describing random walks and boundary conditions :
[HybridTemplateConcept]
public interface IRandomWalker
{
[Kernel]
void Init();
[Kernel]
void Walk(float2 f, out float2 t);
}
[HybridTemplateConcept]
public interface IBoundaryCondition
{
[Kernel]
float Temperature(float x, float y);
}
These interfaces are decorated with
[HybridTemplateConcept] which tells the Hybridizer that these types will be used as type parameters. They can be extended by actual classes such as:
public struct SimpleBoundaryCondition : IBoundaryCondition
{
[Kernel]
public float Temperature(float x, float y)
{
if ((x >= 1.0F && y >= 0.5F) || (x <= 0.0F && y <= 0.5F))
return 1.0F;
return 0.0F;
}
}
Generic types using these interfaces have to tell the hybridizer how they want it to generate template code from generics. This is again done by using attributes:
For example:
[HybridRegisterTemplate(Specialize = typeof(SquareProblem<SimpleWalker, SimpleBoundaryCondition>))]
public class SquareProblem<TRandomWalker, TBoundaryCondition>: I2DProblem
where TRandomWalker : struct, IRandomWalker
where TBoundaryCondition: struct, IBoundaryCondition
{
// other interface methods implementations
// ...
[Kernel]
public void Solve(float2 position)
{
TRandomWalker walker = default(TRandomWalker);
TBoundaryCondition boundaryCondition = default(TBoundaryCondition);
walker.Init(); // generic parameter method call -- will be inlined
float temperature = 0.0F;
float size = (float)_N;
for (int iter = 0; iter < _iter; ++iter)
{
float2 f = position;
while (true)
{
float2 t;
walker.Walk(f, out t); // generic parameter method call -- will be inlined
// when on border, break
if(t.x <= 0.0F || t.y >= size || t.x >= size || t.y <= 0.0F)
{
// generic parameter method call -- will be inlined
temperature += boundaryCondition.Temperature((float)t.x * _h, (float)t.y * _h);
break;
}
// otherwise continue walk
f = t;
}
}
_inner[((int)(position.y - 1)) * (_N - 1) + (int)(position.x - 1)] = temperature * _invIter;
}
}
[HybridRegisterTemplate(Specialize = typeof(TetrisProblem<SimpleWalker, TetrisBoundaryCondition>))]
public class TetrisProblem<TRandomWalker, TBoundaryCondition> : I2DProblem
where TRandomWalker : struct, IRandomWalker
where TBoundaryCondition : struct, IBoundaryCondition
{
// actual interface implementation
}
Results
Dispatchant calls
Virtual functions trigger a callvirt in the MSIL.
IL_005e: callvirt instance void MonteCarloHeatEquation.I2DProblem::Solve
Profiling the generated code with nvvp shows us that a vtable is generated by the Hybridizer (ensuring the right method is called):
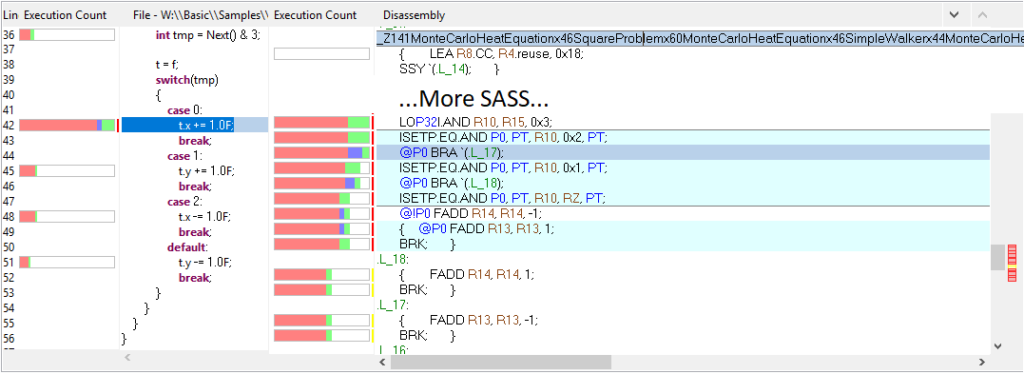
Generics and templates
On the other hand, IRandomWalker and IBoundaryCondition type parameters are mapped to templates. Their methods are therefore inlined, as shown in this nvvp profiling:
By the way: the images above show that your C# code is linked to the sass in the profiler. See our post about debugging and profiling
Conclusion
With few restrictions, you can safely use generics type parameters and dispatchant calls in your C# code. Hybridizer will map that to the correct concept (vtable or template) as your required for.
Dispatchant calls give you full flexibility of an inheritance hierarchy, but come at a performance cost. On the other hand, generics deliver full performance (inlined calls), as long as the right metadata has been provided.
Expm1 Benchmark
This benchmark aims at measuring the floating point performance of the architecture. We use a Taylor expansion of the Expm1 function (exponential of x minus one), at some degree (13 in our case), without any branching. The number of floating point operations, whether it be addition, multiply or fused multiply and add (counted as a single flop in our case) is known ab initio.
We compute the evaluation of that function twelve times to avoid any compute/memory bound unknown hence being sure the calculations are compute bound.
double expm1(double x)
{
return ((((((((((((((15.0 + x)
* x + 210.0)
* x + 2730.0)
* x + 32760.0)
* x + 360360.0)
* x + 3603600.0)
* x + 32432400.0)
* x + 259459200.0)
* x + 1816214400.0)
* x + 10897286400.0)
* x + 54486432000.0)
* x + 217945728000.0)
* x + 653837184000.0)
* x + 1307674368000.0)
* x * 7.6471637318198164759011319857881e-13;
}
We evaluate the function twelve times on a large array of values to exploit parallelism. Depending on the architecture and the flavor of the transformation, vectorization may occur.
We wrote the code in C# and generate target code using Hybridizer. On the other hand, we try to write the best native code for the target architecture. For Intel and IBM targets, code is written in C++ using intrinsics and not raw assembly. For CUDA targets, code is written in plain CUDA. We measure performance of both versions, and see how Hybridizer performs relatively to handwritten code.
| Architecture | Generated | Handwritten | Ratio |
|---|---|---|---|
| NVIDIA- P100 | 1954.7 | 2360.6 | 82.8% |
| NVIDIA – K20C | 505 | 551.1 | 91.6% |
| INTEL – XEON PHI – 7210 | 912.5 | 1003.3 | 90.9% |
| INTEL – Xeon E5 1620 v3 – 3.5 GHz | 60.8 | 84.9 | 71.6% |
| INTEL – Core i7 6700 – 3.4 GHz | 88.1 | 104.5 | 84.3% |
| IBM – POWER8 (2S) | 188.2 | 220.1 | 85.5% |
It can be noticed that on Broadwell (Xeon E5 1620), reached performance is quite far from peak. This is due to the fused-multiply-add instruction latency, which is 5 for a 0.5 throughput. That means we need to enqueue 10 independent instructions to saturate the pipeline. None of the back-end compilers we tried was capable of correctly interleave enough instructions. To reach peak on those architectures, it seems mandatory to write raw assembly. This will be further detailed in a dedicated blog post.
From C# to SIMD : Numerics.Vector and Hybridizer
System.Numerics.Vector is a library provided by .Net (as a nuget package), which tries to leverage SIMD instruction on target hardware. It exposes a few value types, such as Vector<T>, which are recognized by RyuJIT as intrinsics.
Supported intrinsics are listed in the core-clr github repository.
This allows C# SIMD acceleration, as long as code is modified to use these intrinsic types, instead of scalar floating point elements.
On the other hand, Hybridizer aims to provide those benefits without being intrusive in the code (only metadata is required).
We naturally wanted to test if System.Numerics.Vector delivers good performance, compared to Hybridizer.
We measured that Numerics.Vector provides good speed-up over C# code as long as no transcendental function is involved (such as Math.Exp), but still lags behind Hybridizer. Because of the lack of some operators and mathematical functions, Numerics can also generate really slow code (when AVX pipeline is broken). In addition, code modification is a heavy process, and can’t easily be rolled back.
We wrote and ran two benchmarks, and for each of them we have four versions:
- Simple C# scalar code
- Numerics.Vector
- Simple C# scalar code, hybridized
- Numerics.Vector, hybridized
Processor is a core i7-4770S @ 3.1GHz (max measured turbo in AVX mode being 3.5GHz). Peak flops is 224 GFlop/s, or 112 GCFlop/s, if we count FMA as one (since our processor supports it).
Compute bound benchmark
This is a compute-intensive benchmark. For each element of a large double precision array (8 millions elements: 67MBytes), we iterate twelve times the computation of an exponential’s Taylor expansion (expm1). This is largely enough to enter the compute-bound world, by hiding memory operations latency behind a full bunch of floatin point operations.
Scalar code is simply:
[MethodImpl(MethodImplOptions.AggressiveInlining)]
public static double expm1(double x)
{
return ((((((((((((((15.0 + x)
* x + 210.0)
* x + 2730.0)
* x + 32760.0)
* x + 360360.0)
* x + 3603600.0)
* x + 32432400.0)
* x + 259459200.0)
* x + 1816214400.0)
* x + 10897286400.0)
* x + 54486432000.0)
* x + 217945728000.0)
* x + 653837184000.0)
* x + 1307674368000.0)
* x * 7.6471637318198164759011319857881e-13;
}
[MethodImpl(MethodImplOptions.AggressiveInlining)]
public static double twelve(double x)
{
return expm1(expm1(expm1(expm1(expm1(expm1(expm1(expm1(expm1(expm1(expm1(x)))))))))));
}
on which we added the AggressiveInlining attribute to help RyuJit to merge operations at JIT time.
The Numerics.Vector version of the code is quite the same:
[MethodImpl(MethodImplOptions.AggressiveInlining)]
public static Vector<double> expm1(Vector<double> x)
{
return ((((((((((((((new Vector<double>(15.0) + x)
* x + new Vector<double>(210.0))
* x + new Vector<double>(2730.0))
* x + new Vector<double>(32760.0))
* x + new Vector<double>(360360.0))
* x + new Vector<double>(3603600.0))
* x + new Vector<double>(32432400.0))
* x + new Vector<double>(259459200.0))
* x + new Vector<double>(1816214400.0))
* x + new Vector<double>(10897286400.0))
* x + new Vector<double>(54486432000.0))
* x + new Vector<double>(217945728000.0))
* x + new Vector<double>(653837184000.0))
* x + new Vector<double>(1307674368000.0))
* x * new Vector<double>(7.6471637318198164759011319857881e-13);
}
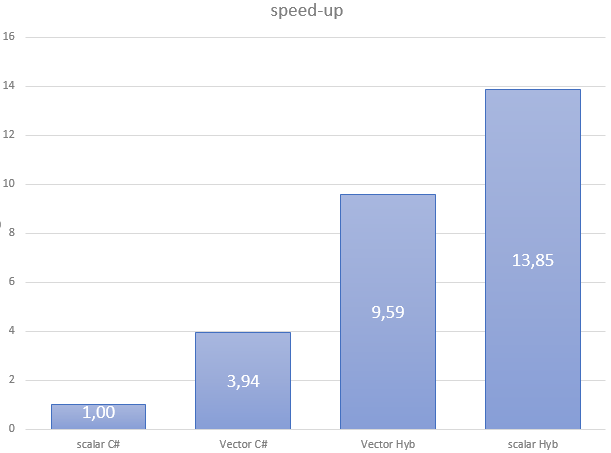
The four versions of this code give the following performance results:
| Flavor | Scalar C# | Vector C# | Vector Hyb | Scalar Hyb |
| GCFlop/s | 4.31 | 19.95 | 41.29 | 59.65 |
As stated, Numerics.Vector delivers a close to 4x speedup from scalar. However, performance is far from what we reach with the Hybridizer. If we look at generated assembly, it’s quite clear why:
vbroadcastsd ymm0,mmword ptr [7FF7C2255B48h] vbroadcastsd ymm1,mmword ptr [7FF7C2255B50h] vbroadcastsd ymm2,mmword ptr [7FF7C2255B58h] vbroadcastsd ymm3,mmword ptr [7FF7C2255B60h] vbroadcastsd ymm4,mmword ptr [7FF7C2255B68h] vbroadcastsd ymm5,mmword ptr [7FF7C2255B70h] vbroadcastsd ymm7,mmword ptr [7FF7C2255B78h] vbroadcastsd ymm8,mmword ptr [7FF7C2255B80h] vaddpd ymm0,ymm0,ymm6 vmulpd ymm0,ymm0,ymm6 vaddpd ymm0,ymm0,ymm1 vmulpd ymm0,ymm0,ymm6 vaddpd ymm0,ymm0,ymm2 vmulpd ymm0,ymm0,ymm6 vaddpd ymm0,ymm0,ymm3 vmulpd ymm0,ymm0,ymm6 vaddpd ymm0,ymm0,ymm4 vmulpd ymm0,ymm0,ymm6 vaddpd ymm0,ymm0,ymm5 vmulpd ymm0,ymm0,ymm6 vaddpd ymm0,ymm0,ymm7 vmulpd ymm0,ymm0,ymm6 vaddpd ymm0,ymm0,ymm8 vmulpd ymm0,ymm0,ymm6 ; repeated
Fused multiply add are not reconstructed, and constant operands are reloaded from constant pool at each expm1 invokation. This leads to high registry pressure (for constants), where memory operands could save some.
Here is what the Hybridizer generates from scalar code:
vaddpd ymm1,ymm0,ymmword ptr [] vfmadd213pd ymm1,ymm0,ymmword ptr [] vfmadd213pd ymm1,ymm0,ymmword ptr [] vfmadd213pd ymm1,ymm0,ymmword ptr [] vfmadd213pd ymm1,ymm0,ymmword ptr [] vfmadd213pd ymm1,ymm0,ymmword ptr [] vfmadd213pd ymm1,ymm0,ymmword ptr [] vfmadd213pd ymm1,ymm0,ymmword ptr [] vfmadd213pd ymm1,ymm0,ymmword ptr [] vfmadd213pd ymm1,ymm0,ymmword ptr [] vfmadd213pd ymm1,ymm0,ymmword ptr [] vfmadd213pd ymm1,ymm0,ymmword ptr [] vfmadd213pd ymm1,ymm0,ymmword ptr [] vfmadd213pd ymm1,ymm0,ymmword ptr [] vmulpd ymm0,ymm0,ymm1<br /> vmulpd ymm0,ymm0,ymmword ptr [] vmovapd ymmword ptr [rsp+0A20h],ymm0 ; repeated
This reconstructs fused multiply-add, and leverages memory operands to save registers.
Why are we not to peak performance (112GCFlops)? That is because Haswell has two pipelines for FMA, and a latency of 5 (see intel intrinsic guide. To reach peak performance, we would need to interleave 2 independant FMA instruction at each cycle. This could be done by reordering instructions, since reorder buffer is not long enough to execute instructions too far in the pipeline. LLVM, our backend compiler, is not capable of such reordering. To get better performance, we unfortunately have to write assembly by hand (which is not exactly what a C# programmer expects to do in the morning).
Invoke transcendentals
In this second benchmark, we need to compute the exponential of all the components of a vector. To do that, we invoke Math.Exp.
Scalar code is:
[EntryPoint]
public static void Apply_scal(double[] d, double[] a, double[] b, double[] c, int start, int stop)
{
int sstart = start + threadIdx.x + blockDim.x * blockIdx.x;
int step = blockDim.x * gridDim.x;
for (int i = sstart; i < stop; i += step)
{
d[i] = a[i] * Math.Exp(b[i]) * Math.Exp(c[i]);
}
}
This function is later called in a
Parallel.For construct.
However, Numerics.Vector does not provide a vectorized exponential function. Therefore, we have to write our own:
[IntrinsicFunction("hybridizer::exp")]
[MethodImpl(MethodImplOptions.AggressiveInlining)]
public static Vector<double> Exp(Vector<double> x)
{
double[] tmp = new double[Vector<double>.Count];
for(int k = 0; k < Vector<double>.Count; ++k)
{
tmp[k] = Math.Exp(x[k]);
}
return new Vector<double>(tmp);
}
As a glance, we can see the problems: each exponential will first break the AVX context (which cost tens of cycles), and trigger 4 function calls instead of one.
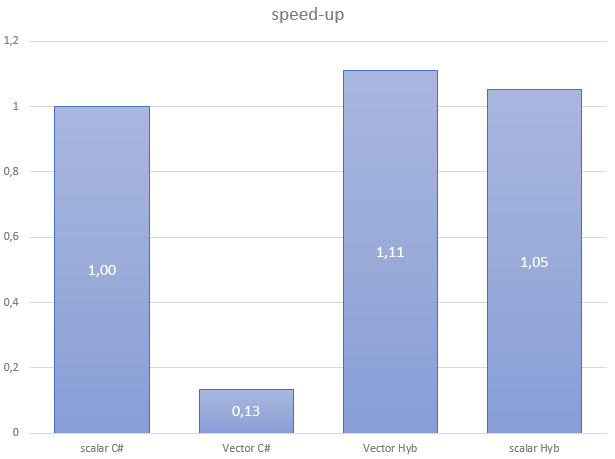
With no surprise, this code performs really badly:
| Flavor | Scalar C# | Vector C# | Vector Hyb | Scalar Hyb |
| GB/s | 13.42 | 1.80 | 14.91 | 14.13 |
If we look at the generated assembly, it confirms what we suspected (context switched, and ymm register splitting):
vextractf128 xmm9,ymm6,1 vextractf128 xmm10,ymm7,1 vextractf128 xmm11,ymm8,1 call 00007FF8127C6B80 // exp vinsertf128 ymm8,ymm8,xmm11,1 vinsertf128 ymm7,ymm7,xmm10,1 vinsertf128 ymm6,ymm6,xmm9,1
Branching
Branch are expressed using if or ternary operators in scalar code. However, those are not available in Numerics.Vector, since the code is manually vectorized.
Branches must be expressed using ConditionalSelect, which leads to code:
public static Vector<double> func(Vector<double> x)
{
Vector<long> mask = Vector.GreaterThan(x, one);
Vector<double> result = Vector.ConditionalSelect(mask, x, one);
return result;
}
As we can see, expressing conditions with Numerics.Vector is not intuitive, intrusive, and bug prone. It’s actually the same as writing AVX compiler intrinsics in C++. On the other hand, Hybridizer supports conditions, which allow you to write the above code this way:
[Kernel]
public static double func(double x)
{
if (x > 1.0)
return x;
return 1.0;
}
Conclusion
Numerics.Vector gives easily reasonable performances on simple code (no branches, no function calls). Speed-up is what we expect (vector unit width) on simple code. However, it’s time-consuming and error-prone to express conditions, and performance is completely broken as soon as some Jitter Intrinsic is missing (such as exponential).