Altimesh

Author: regis portalez

Image processing on a GPU with AForge

Posted on by regis portalez

AForge is a popular .Net library for image processing and computer vision. It features a lot of image filters, noise generators, or other image-related algorithms.
Since it’s written in C#, and given the very parallel nature of most of image processing algorithms, we tried to hybridize some of them.
AForge code make heavy use of dot net unsafe, which is supported by the Hybridizer.

We chose two examples to illustrate hybridizer’s capabilities. First is Perlin noise, a highly compute intensive noise generator, and second is AdaptiveSmoothing, a latency bound image filter.

Perlin noise

Perlin noise is written for double precison in AForge, and we test on a GTX 1080 Ti, which has almost no double precision arithmetic units. We therefore first cloned the Perlin noise algorithm and made a PerlinNoiseFloat class, in which we just replaced “double” by “float”, without changing a single bit of the code structure or algorithm implementation.
However, Perlin noise makes use of Cosine function, which is only available for double in C#. We replaced Math.Cos by an Intrinsic function, mapped to cosf from C99 standard:

[IntrinsicFunction("cosf")]
public static float cosf(float x)
{
    return (float)Math.Cos(x);
}

The main function is a simple cuda-like loop, other mathematical functions being mapped to their C99 counterparts with the default builtin file:

[EntryPoint]
public static void ComputePerlin(PerlinNoiseFloat noise, float[] image, int width, int height)
{
    for (int y = threadIdx.y + blockDim.y * blockIdx.y; y < height; y += blockDim.y * gridDim.y)
    {
        for (int x = threadIdx.x + blockDim.x * blockIdx.x; x < width; x += blockDim.x * gridDim.x)
        {
            image[y*width + x] = Math.Max(0.0f, Math.Min(1.0f, noise.Function2D(x, y) * 0.5f + 0.5f));
        }
    }
}

PerlinNoiseFloat is defined in a separate assembly (AForge.Imaging) in which we didn’t put any custom attributes. Given noise.Function2D is invoked by an EntryPoint, hybridizer infers that it must be a __device__ function, and that code should be generated (call graph is walked by the Hybridizer).

We then invoke this function by wrapping the parent type using HybRunner:

PerlinNoiseFloat noise = new PerlinNoiseFloat();
noise.Octaves = 16;
const int height = 2048;
const int width = 2048;

// generate clouds effect
float[] texture = new float[height*width];
HybRunner runner = HybRunner.Cuda("TestRun_CUDA.dll").SetDistrib(32, 32, 16, 16, 1, 0);
dynamic wrapped = runner.Wrap(new Program());

wrapped.ComputePerlin(noise, texture, width, height);

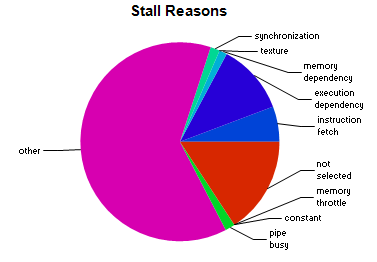
This saturates the compute units of the 1080 Ti, as we can see in this nvvp report:

Stall reasons being mostly Other and Not Selected, for which we hqve no documentation to address:

Result image is here:

Adaptive Smoothing

Adaptive smoothing is a noise removal filter which preserves edges. The kernel operates on 9 pixels (the 8 around, and the current one) and is described here.

To run this filter on the GPU, we had to slightly modify AForge code, since it was really designed and optimized for single-thread CPU. For example, the main loop was written this way:

for ( int y = startYP2; y < stopYM2; y++ )
{
    src += pixelSize2;
    dst += pixelSize2;
    for(int x = startXP2; x < stopXM2; x++)
    {
        for(int i = 0; i < pixelSize; i++, src++, dst++)
            // operations

in which pointers src and dst are incremented. This can’t be multithreaded, or hybridized, since each thread can’t rely on each other to know where to work.
We changed that loop by a CUDA-like loop, with in place addresses calculation:

int ystart = threadIdx.y + blockIdx.y * blockDim.y;
int yinc = blockDim.y * gridDim.y;
int xstart = threadIdx.x + blockIdx.x * blockDim.x;
int xinc = blockDim.x * gridDim.x;

for (int y = startYP2 + ystart; y < stopYM2; y += yinc)
{
    for (int x = startXP2 + xstart; x < stopXM2; x += xinc)
    {
        byte* vsrc = src + srcInitOffset + ...
        byte* vdst = dst + dstInitOffset + ...
        for(int i = 0; i < pixelSize; ++i)
            // operations

We also had to expose single precision exponential function through intrinsic function, mapped to expf from C99 standard:

[IntrinsicFunction("expf")]
public static float expf(float x)
{
    return (float)Math.Exp(x);
}

and do some manual memory management (cudaMalloc/cudaFree/cudaMemcpy). Indeed, unlike arrays, pointers cannot be automatically marshalled (memory size is unknown).

The main loop (ready for hybridization) looks this way:

[EntryPoint]
public static unsafe void Apply(int srcStride, int dstStride, int pixelSize, int srcOffset, int dstOffset, int startX, int startY, int stopX, int stopY, float invf, byte* src, byte* dst)
{
    int startXP2 = startX + 2;
    int startYP2 = startY + 2;
    int stopXM2 = stopX - 2;
    int stopYM2 = stopY - 2;
    int pixelSize2 = 2 * pixelSize;
    int srcInitOffset = srcStride * 2 + (startY * srcStride + startX * pixelSize) + pixelSize2;
    int dstInitOffset = dstStride * 2 + (startY * dstStride + startX * pixelSize) + pixelSize2;
    int incx = pixelSize;
    int incsrcy = srcOffset + 2 * pixelSize2;
    int incdsty = dstOffset + 2 * pixelSize2;

<pre><code>for (int y = startYP2 + threadIdx.y + blockIdx.y * blockDim.y; y < stopYM2; y += blockDim.y * gridDim.y)
{
    for (int x = startXP2 + threadIdx.x + blockDim.x * blockIdx.x; x < stopXM2; x += blockDim.x * gridDim.x)
    {
        byte* vsrc = src + srcInitOffset
                         + (y - startYP2) * incsrcy + (y - startYP2) * (stopXM2 - startXP2) * incx 
                         + (x - startXP2) * incx;
        byte* vdst = dst + dstInitOffset 
                         + (y - startYP2) * incdsty + (y - startYP2) * (stopXM2 - startXP2) * incx 
                         + (x - startXP2) * incx;
        for (int i = 0; i < pixelSize; i++, vsrc++, vdst++)
        {
            // gradient and weights
            float gx, gy, weight, weightTotal, total;

            weightTotal = 0;
            total = 0;

            // original formulas for weight calculation:
            // w(x, y) = exp( -1 * (Gx^2 + Gy^2) / (2 * factor^2) )
            // Gx(x, y) = (I(x + 1, y) - I(x - 1, y)) / 2
            // Gy(x, y) = (I(x, y + 1) - I(x, y - 1)) / 2
            //
            // here is a little bit optimized version

            // x - 1, y - 1
            gx = vsrc[-srcStride] - vsrc[-pixelSize2 - srcStride];
            gy = vsrc[-pixelSize] - vsrc[-pixelSize - 2 * srcStride];
            weight = expf((gx * gx + gy * gy) * invf);
            total += weight * vsrc[-pixelSize - srcStride];
            weightTotal += weight;

            // x, y - 1
            gx = vsrc[pixelSize - srcStride] - vsrc[-pixelSize - srcStride];
            gy = vsrc[0] - vsrc[-2 * srcStride];
            weight = expf((gx * gx + gy * gy) * invf);
            total += weight * vsrc[-srcStride];
            weightTotal += weight;

            // x + 1, y - 1
            gx = vsrc[pixelSize2 - srcStride] - vsrc[-srcStride];
            gy = vsrc[pixelSize] - vsrc[pixelSize - 2 * srcStride];
            weight = expf((gx * gx + gy * gy) * invf);
            total += weight * vsrc[pixelSize - srcStride];
            weightTotal += weight;

            // x - 1, y
            gx = vsrc[0] - vsrc[-pixelSize2];
            gy = vsrc[-pixelSize + srcStride] - vsrc[-pixelSize - srcStride];
            weight = expf((gx * gx + gy * gy) * invf);
            total += weight * vsrc[-pixelSize];
            weightTotal += weight;

            // x, y
            gx = vsrc[pixelSize] - vsrc[-pixelSize];
            gy = vsrc[srcStride] - vsrc[-srcStride];
            weight = expf((gx * gx + gy * gy) * invf);
            total += weight * (vsrc[0]);
            weightTotal += weight;

            // x + 1, y
            gx = vsrc[pixelSize2] - vsrc[0];
            gy = vsrc[pixelSize + srcStride] - vsrc[pixelSize - srcStride];
            weight = expf((gx * gx + gy * gy) * invf);
            total += weight * vsrc[pixelSize];
            weightTotal += weight;

            // x - 1, y + 1
            gx = vsrc[srcStride] - vsrc[-pixelSize2 + srcStride];
            gy = vsrc[-pixelSize + 2 * srcStride] - vsrc[-pixelSize];
            weight = expf((gx * gx + gy * gy) * invf);
            total += weight * vsrc[-pixelSize + srcStride];
            weightTotal += weight;

            // x, y + 1
            gx = vsrc[pixelSize + srcStride] - vsrc[-pixelSize + srcStride];
            gy = vsrc[2 * srcStride] - vsrc[0];
            weight = expf((gx * gx + gy * gy) * invf);
            total += weight * vsrc[srcStride];
            weightTotal += weight;

            // x + 1, y + 1
            gx = vsrc[pixelSize2 + srcStride] - vsrc[srcStride];
            gy = vsrc[pixelSize + 2 * srcStride] - vsrc[pixelSize];
            weight = expf((gx * gx + gy * gy) * invf);
            total += weight * vsrc[pixelSize + srcStride];
            weightTotal += weight;

            // save destination value
            *vdst = (weightTotal == 0.0F) ? vsrc[0] : (byte)min(total / weightTotal, 255.0F);
        }
    }
}
</code></pre>

}

We run this filter on a fullHD image (1080p):

and we get the following level of performance:

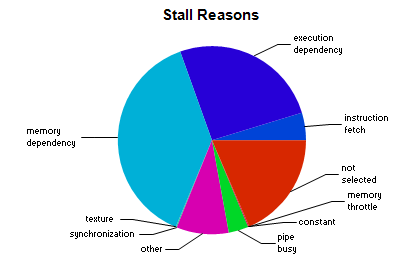
with 98.2% of warp execution efficiency.

Stall reasons are:

mostly memory dependency and execution dependency.

Occupancy limiter is registers with 40 registers per thread.

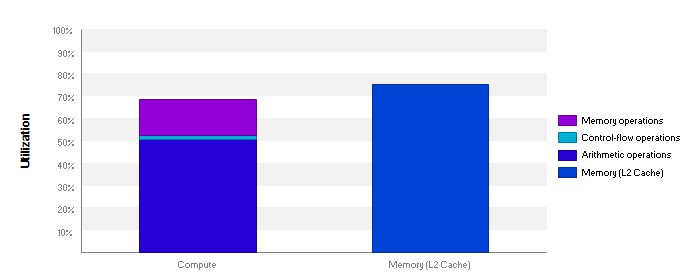
Given both compute and memory are highly used, the kernel is memory-latency bound, which is difficult to optimize further without being really intrusive in the code. We could get some improvement by processing a group of pixels simultaneously, or make use of Surfaces to benefit from 128 bits loads and stores in GPU memory.

Conclusion

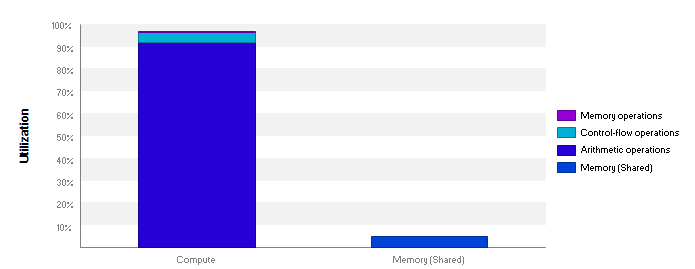
In this post we demonstrated how we can take production-level C# code (with advanced features such as unsafe code) and run it on a GPU with the Hybridizer. In the case of Perlin, we don’t even have to modify the third-part library, since writing a kernel in our application will make Hybridizer automatically walk through dependencies and generate the appropriate code.
This code is completely compute bound on a GPU, and that is what we observe. In the other case (Adaptive smoothing), we solely had to modify the pointer indexing calculation scheme which is anyway necessary to make loop iterations independent. This change would be required to benefit from any modern hardware.

Hybridize A Large Image Processing Library

Posted on by regis portalez

AForge is a great Image Processing and Vision .Net library.
We developed a few example applications making use of AForge and Hybridizer. Those two examples are:

  • A kernel function in application code which triggers the hybridization of AForge itself. This shows that dependencies are pulled by the Hybridizer with no user intervention. On Perlin noise code, we reach peak compute performance on a 1080 Ti.
  • Adaptive smoothing. We had to change AForge code to enable parallel processing (addresses computation). We then call it from a plain C# application code. We have therefore an hybridized library used transparently from the application code. Kernel appears to be memory-latency bound on a 1080 Ti.

Read more

Mandelbrot with Hybridizer

Posted on by regis portalez

We describe here the implementation of Mandelbrot fractal image generation using Hybridizer. The language of choice is C#, and implementation is done using 32-bits precision arithmetic.

Mandelbrot set is the set of values c for which the sequence:

\(\left\{\begin{array}{l}
z_0 = 0\\
z_{n+1}= z_n^2 + c
\end{array}\right.\)

remains bounded in the complex plane.
It happens an equivalent definition is:

\(\limsup_\limits{n\rightarrow+\infty}z_n \leq 2\)

That means that while calculating \(z_n\) values exceeds \(2\) at any iteration, the point c is not in the set.

C# implementation

In other words, this can be simulated via this code:

public static int IterCount(float cx, float cy)
{
    int result = 0;
    float x = 0.0f;
    float y = 0.0f;
    float xx = 0.0f, yy = 0.0f;
    while (xx + yy <= 4.0f && result < maxiter) // are we out of control disk?
    {
        xx = x * x;
        yy = y * y;
        float xtmp = xx - yy + cx;
        y = 2.0f * x * y + cy; // computes z^2 + c
        x = xtmp;
        result++;
    }

    return result;
}

which has to be run for every point (cx, cy) in the complex plane.
To produce an output image, we therefore compute IterCount for every pixel in the square \([-2,2]\times[-2,2]\), discretized as a \(N\times N\) square grid:

public static void Run(int[] light)
{
    for (int i = 0; i < N; i += 1)
    {
        for (int j = 0; j < N; j += 1)
        {
            float x = fromX + i * h;
            float y = fromY + j * h;
            light[i* N + j] = IterCount(x, y);
        }
    }
}

where N, h, fromX and fromY are application parameters.
We here compute a \(2048\times 2048\) image using C# on a core i7-4770S @ 3.10GHz.
This unoptimized versions runs in 420 milliseconds, yielding

9.986 millions pixels / second

Its crystal clear that this code is embarrassingly parallel, since all pixels are independant from each other.

A first trivial optimization would therefore to make the first loop parallel:

public static void Run(int[] light)
{
    Parallel.For(0, N, (i) => {
        for (int j = 0; j < N; j += 1)
        {
            float x = fromX + i * h;
            float y = fromY + j * h;
            light[i * N + j] = IterCount(x, y);
        }
    });
}

This second version runs in 67 milliseconds, giving:

62.6 millions pixels / second

Run on the GPU

In order to run that on a GPU, we just need to decorate the Run method with EntryPointAttribute:

[EntryPoint("run")]
public static void Run(int[] light)
{
    Parallel.For(0, N, (i) => {
        for (int j = 0; j < N; j += 1)
        {
            float x = fromX + i * h;
            float y = fromY + j * h;
            light[i * N + j] = IterCount(x, y);
        }
    });
}

and some boilerplate code to invoke the generated method:

HybRunner runner = HybRunner.Cuda("Mandelbrot_CUDA.dll").SetDistrib(N, 128);
wrapper = runner.Wrap(new Program());
wrapper.Run(light_cuda);

This modified code runs on the GPU (a 1080 Ti) in 10.6 milliseconds (32 when counting the memory copies), giving:

395.7 millions pixels / second

Further optimization

Launching a block per image line is highly suboptimal, due to the unevenly distribute nature of the computations. For example, threads at the square’s border will immediately converge, while those on the set will take the longest runtime.
This can be seen by profiling the above code using Nsight:

As we can see, half of multiprocessors are idle.

We can instead distribute the work more evenly by using a 2D grid of relatively small blocks.

Fortunately, Hybridizer supports CUDA-like parallelism, so we can modify our entrypoint this way:

[EntryPoint("run")]
public static void Run(int[] light)
{
    for (int i = threadIdx.y + blockDim.y * blockIdx.y; i < N; i += blockDim.x * gridDim.x)
    {
        for (int j = threadIdx.x + blockDim.x * blockIdx.x; j < N; j += blockDim.y * gridDim.y)
        {
            float x = fromX + i * h;
            float y = fromY + j * h;
            light[i * N + j] = IterCount(x, y);
        }
    }
}

and run it with a 2D grid:

HybRunner runner = HybRunner.Cuda("Mandelbrot_CUDA.dll").SetDistrib(32, 32, 16, 16, 1, 0);

The modified code runs now in 920 microseconds on the GPU, meaning:

4.56 billions pixels / second

If we profile the newly generated kernel, we get:

main stall reason being “Other” with 69% followed by instruction fetch for only 5% of not eligible warps.
It’s reasonable to not try further optimization.

Conclusion

In this post we presented a basic usage of hybridizer, from unoptimal c# to highly efficient generated cuda code. We started by optimize our c# code and the migrated it seamlessly to CUDA.
We then optimized our c# code for CUDA GPUs, until we reached a close to peak performance level.