Hybridizer is a compiler that lets you run a single version of your C# or Java code on any harware.
In this tutorial, we will explain how to create a first project in C# targeting GPU. We will illustrate with hybridizer essentials.
Warning/Disclaimer
We don’t support the entire C# language or .Net Framework. Main known limitations are:
- Heap allocation (new A()) from device thread (except for arrays)
- System.Collection is not supported
- string type is not supported
Prerequisites
Software
You first need to install the following software:
- Visual Studio 2012, 2013, 2015 or 2017. Warning, in Visual Studio 2017 with CUDA 9.2 or earlier you need to install v140 toolset from Visual Studio Installer.
- Ensure your Visual installation supports C++ and not just C#.
- CUDA toolkit 8.0, 9.0, 9.1, 9.2 or 10.0
- Any version of the Hybridizer, including the free version, Hybridizer Essentials
License
You need to request a Hybridizer Subscription.
Subscriptions are our new licensing model for Hybridizer Essentials. They can migrate from one machine to another (only one machine being authorized at a time).
Trial are unique and attached to your email address, while you can purchase as many commercial subscriptions as you want.
Either you already purchased one, or you can request a trial for Hybridizer Essentials. To do that, click on Hybridizer->License Settings in Visual Studio:
If you opted for the trial, provide you email address and click Subscribe:
You should receive your license in your mailbox soon. If not, please contact us or create an issue on github.
Open your mailbox, and select the license text as follow:
Paste this text in the license textbox in Hybridizer Configuration, and click Refresh License.
Hybridizer should validate the subscription, assign a license to your machine, and tell you the following:
First project
You have two options:
Brand new project
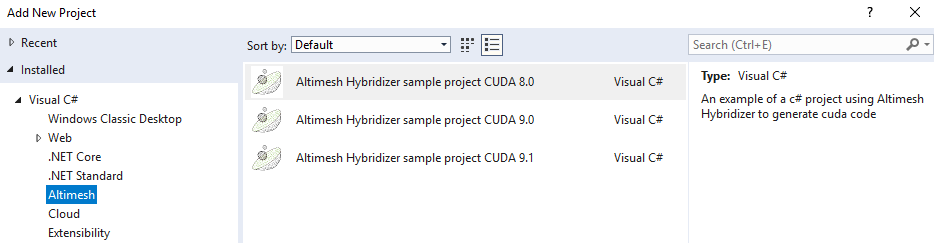
From Visual Studio, click File, New, Project. Choose C#, Altimesh:
Build C# project, then native generated project, and run.
From existing C# project
First create or open and existing C# console application.
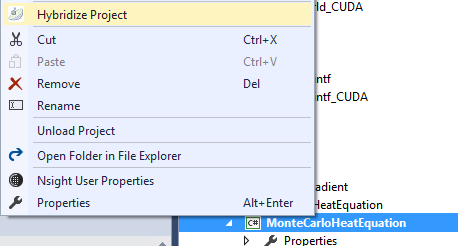
Right click on the project in the solution explorer, and select “Hybridize Project”:
This step will create a native CUDA project and add it your solution. It will handle the files generated by Hybridizer from your managed C# project.
Fill the requested fields and click “Generate”:
If everything worked correctly, several things happened in the background:
- Your C# project now references Hybridizer.Runtime.CUDAImports. This assembly provides all the necessary attributes to hybridize methods, a CUDA wrapper, and a memory marshaller. We will come back on those in later posts.
- A native project has been created and added to your solution. This project references two files, hybridizer.generated.cpp and hybridizer.wrappers.cu. The first one will contain a cubin module. The second will export native symbols.
- If not already existing, an x64 platform configuration has been added to your solution.
Before building anything, change configuration to x64. 32 bit support is indeed being deprecated by NVIDIA, and nvrtc requires 64 bits.
Create a kernel
In your main class, add the following code:
[EntryPoint]
public static void Hello()
{
Console.Out.Write("Hello from GPU");
}
The EntryPoint attribute tells the hybridizer to generate a CUDA kernel, as if you wrote:
__global__ void Hello() {
printf("Hello from GPU\n");
}
You can now build the C# project, and the the satellite project. You can inspect generated file to see what hybridizer generated:
- hybridizer.generated.cpp contains a big array of bytes, which is the device code of your kernel.
- hybridizer.wrappers.cu exports a symbol:
extern "C" DLL_PUBLIC int ConsoleApplication3x46Programx46Hello_ExternCWrapper_CUDA(...) { CUresult cures ; if (__hybridizer__gs_module.module_data == 0) { cures = cuModuleLoadData (&(__hybridizer__gs_module.module), __hybridizer_cubin_module_data) ; if (cures != CUDA_SUCCESS) return (int)cures ; } CUfunction __hybridizer__cufunc ; cures = cuModuleGetFunction (&__hybridizer__cufunc, __hybridizer__gs_module.module, "ConsoleApplication3x46Programx46Hello") ; if (cures != CUDA_SUCCESS) return (int)cures ; // more generated code ... cures = cuLaunchKernel (__hybridizer__cufunc, ...) ; if (cures != CUDA_SUCCESS) return (int)cures ; int cudaLaunchRes = (int)::cudaPeekAtLastError (); if (cudaLaunchRes != 0) return cudaLaunchRes; int __synchronizeRes = (int)::cudaDeviceSynchronize () ; return __synchronizeRes ; }
Run it
In your main method, add the following boilerplate code:
static void Main(string[] args)
{
cuda.DeviceSynchronize();
HybRunner runner = HybRunner.Cuda("ConsoleApplication3_CUDA.vs2015.dll").SetDistrib(1, 2);
runner.Wrap(new Program()).Hello();
}
with the appropriate generated dll name. This code:
- registers the generated dll as a CUDA dll: HybRunner.Cuda(“ConsoleApplication3_CUDA.vs2015.dll”)
- configure kernels calls to run with 1 block of 2 threads: SetDistrib(1, 2)
- registers the current object as a kernel container: runner.Wrap(new Program())
- runs the generated method.
Then run:
Congratulations! You just successfully ran your first C# kernel on the GPU!